前言

读江辉有《拓扑学》[1]笔记

1. 引言

1.1 一笔画问题和哥尼斯堡七桥问题

1.2 欧拉(Euler)示性数

1.3 图的可平面化处理问题

  • 对于由顶点和线构成的图，如果每个顶点间都有线相连，则这样的图称之为完全图。下图中的K5是完全图，K33不是完全图
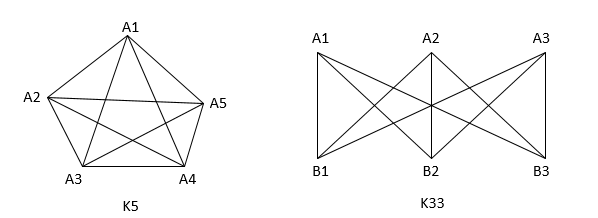
    first

所谓图的可平面化问题就是：一个图应当满足什么条件，才可以在平面上不自交的被画出来?这也就是通常说的可嵌入平面的问题。这里说的不自交指的是不同的线不会相交，至于线如何回还转曲不加限制。

  • Kuratowsky定理
    • 一个图G可以嵌入平面当且仅当G不含有K5或K33同构的子图
    • 有意思的是，K33虽然不能嵌入平面，却可以嵌入Mobius带。

1.4 扭结论(Knot theory)研究

1.5 四色问题

2. 点集拓扑学

2.1 预备知识

2.1.1 集合代数与关系
  • X所有子集构成的集族，称为X的幂集，用2^X表示
  • 笛卡尔积: \(X\times Y=\{(x,y):x\in X,y\in Y\}\). \(X\times Y\)的任一子集R称为X到Y的一个关系。若\((x,y)\in R\)，则称x与y是R-相关的，也记为xRy。若R是X到Y的一个关系，则其定义集为\(\{x\in X: \exists y\in Y, xRy\}\)(为方便也常记为DR)，也称为定义域。而其值集则定义为\(\{y\in Y: \exists x\in X, xRy\}\)。
2.1.2 函数与等价关系
  • 包含映射(含入映射)
  • 自反&对称&传递\(\Rightarrow\)等价关系
  • 商集, 自然映射
  • 划分
2.1.3 序关系与选择公理
  • 设R是X上的一个关系，如果\(xRy\wedge yRx\)，则必有x=y，那么我们称R在X上是反对称的。X上的一个自反、反对称且传递的关系R就称为X上的一个偏序。当R是X上的一个偏序时，偶对(X,R)称为一个偏序集。在偏序关系R明确的情况下，有时也简称X为一个偏序集。偏序关系常用≤来表示
  • 全序(也称线性序)；全序集(或线性序集)，也称为链
  • 良序；良序集
  • 闭区间，左闭右开区间，开区间，闭右射线，开右射线，区间，诱导偏序，偏序子集
  • 选择公理\(\Leftrightarrow\)Zermelo良序定理\(\Leftrightarrow\)Teichmuller-Tukey引理\(\Leftrightarrow\)Kuratowski-Zorn引理
2.1.4 集合的可数性

如果集合A的元素是只有有限个，就称它是有限集，否则为无限集。如今我们把能与自然数集形成一一对应的集合称为可数无限集(也称可列集)，而把有限集和可数无限集统称为可数(countable)集，也就是说，能够与自然数集的某个子集形成一一对应的集合都称为可数集。不是可数集的集合不可数

2.1.5 基数简介
  • 定义：如果在集合A和集合B之间存在一一对应\(f: A\rightarrow B\)，则称集合A和集合B是等势的，记为AB。如果存在自然数n使得A{1,2,…,n}，则称集合A是有限的；不是有限的集合就是无限的。如果A~N(正整数集)，则称A是可数无限的(或者可列的)；有限的或可数无限的统称为可数的。
  • 定理：集合间的等势关系是一个等价关系，即对任意集合A,B,C，有：
    • \(A\sim A\)
    • \(A\sim B \Rightarrow B\sim A\)
    • \((A\sim B)\wedge (B\sim C)\Rightarrow A\sim C\)
  • 定义：对于每个集合A，对应一个符号|A|，称为A的基数，它满足以下条件：
    • 如果A~B，则|A|=|B|
    • \(|\varnothing| = 0\)
    • 如果有自然数n使得A~{1,2,…,n}，则|A|=n
    • 显然基数就是通常个数概念的推广
    • ……

3. 拓扑空间的基本概念

3.1 拓扑空间的定义

设X是一个非空集合，其子集族\(\Im \subset 2^X\)称为X上的一个拓扑，如果它满足：

  • \(X,\varnothing\)均为\(\Im\)中元素
  • \(\Im\)中任意多个元素的并集仍为\(\Im\)中元素(也称\(\Im\)对并运算封闭)
  • \(\Im\)有限个元素的交集仍为\(\Im\)中元素(也称\(\Im\)对有限交运算封闭)
  • 此外，偶对\((X,\Im)\)称为一个拓扑空间，通常简记为X

这时拓扑空间的每一个元叫做开集，同样还可以定义闭集(后续会说)，所以也可以用闭集来定义拓扑空间。

3.2 度量拓扑

  • 非空集合X上的一个度量d是指一个满足如下三条度量公理的映射\(d: X\times X \rightarrow R\)
      1. 非负性：\(d(x,y)\geq 0,\forall x,y\in X\), 等号当且仅当x=y时成立
      1. 对称性：\(d(x,y)=d(y,x),\forall x,y\in X\)
      1. 三角不等式：\(d(x,z)\leq d(x,y)+d(y,z),\forall x,y\in X\)
  • 示例：
      1. 在n维欧式空间\(\mathbb{R}^n\),如下定义的映射\(d:\mathbb{R}^n \times \mathbb{R}^n\),\(d(x,y)=\parallel x-y\parallel =\sqrt{\sum_{i=1}^{n}(x_i-y_i)^2},\forall x=(x_1,x_2,\cdots,x_n),y=(y_1,y_2,\cdots,y_n)\in \mathbb{R}^n\)是一个度量，称为欧式度量
      1. 在\(C[a,b]\)上，对于两个函数\(f,g\in C[a,b]\)，由\(d(f,g)=\int_a^b|f-g|dx\)定义的映射给出了\(C[a,b]\)上的一个变量
      1. 在任意一个非空集X上，\(d(x,y)=\begin{cases} 0,x=y\\1,x\neq y \end{cases}\forall x,y\in X\)定义了一个度量，这个度量通常称为离散度量
      1. 在集合\(H=\left\{x=(x_1,x_2,\cdots,x_n,\cdots)|\sum_{i=1}^{\infty}x_i^2<+\infty,x_i\in \mathbb{R}\right\}\)上，定义\(d(x,y)=\sqrt{\sum_{i=1}^{\infty}(x_i-y_i)^2},\forall x=(x_1,x_2,\cdots),y=(x_1,y_2,\cdots)\in H\)，则d是H上的一个度量
  • 度量空间：
    对于定义了度量\(d:X\times X\rightarrow \mathbb{R}\)的集合X而言，\(\forall x_0\in X,\forall \epsilon >0\)，称\(B(x_0,\epsilon)=\{x\in X|d(x,x_0)<\epsilon\}\)为以\(x_0\)为中心，\(\epsilon\)为半径的球形领域(开球)，再令\(\Im_d=\{U\subset X|U是X中若干个球形领域的并集\}\)，则很容易验证：\(\Im_d\)是X上的一个拓扑，称为由度量d诱导的拓扑（简称度量拓扑）。此时，拓扑空间\((X,\Im_d)\)通常简记为(X,d)，甚至在不引起混乱的情况下直接记为X，称为度量空间

3.3 拓扑空间的几个基本概念

  • 闭集：拓扑空间中的一个集合F，如果其补集为开集，则称它为闭集
  • 在一个拓扑空间中，能表示为可数多个闭集的并集的集合称为\(F_\sigma -\)集
  • 在一个拓扑空间中，能表示为可数多个闭集的并集的集合称为\(G_\sigma -\)集
  • 集合X的一个非空子集族\(\Sigma\)称为一个\(\sigma -\)环，是指它满足：
      1. 对余运算封闭：\(A\in \Sigma\Rightarrow A^C\in \Sigma\)
      1. 对可数交运算封闭：\(A_i\in \Sigma(i\in \mathbb{N})\Rightarrow \bigcap_{i\in \mathbb{N}}A_i\in \Sigma\)
  • 邻域、内点和内部
  • 聚点与闭包
  • 序列的收敛性

3.4 子空间

Footnotes